
En el 2000 a.C, el Emperador Yu trataba de aplacar al Dios río Lo (el Río Amarillo), que había desbordado sus aguas provocando catástrofes por toda la zona. Para detener la furia de las aguas, el Emperador realizó una serie de ofrendas y sacrificios ante la mirada desesperada de sus súbditos, que veían anegadas todas sus posesiones.
Del río surgió de pronto la Tortuga Divina, que con parsimonia se acercó a las ofrendas del Emperador, las examinó, dio media vuelta y se fue. El mensaje del dios Lo quedaba claro. No era suficiente. Las gentes y los sabios se empezaron a preguntar qué número de sacrificios haría falta para calmar al dios. El emperador permaneció reflexivo un rato, dándole vueltas a los extraños dibujos que había visto sobre el caparazón de la tortuga:

- Dibujos en el caparazón de la Tortuga Divina.
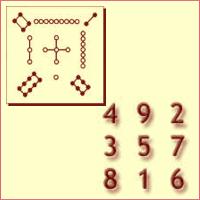
- Traducción a números de los dibujos.
No tardó mucho en darse cuenta de que aquellos puntos unidos por líneas representaban números, por lo que el caparazón de la tortuga podía representarse en una cuadrícula de 3×3 con los números del 1 al 9 tal como los había visto colocados en la espalda del animal. Ahora bien, ¿Cómo habría de colocarse el cuadrado para entender su mensaje?. Bocaarriba, Bocaabajo?.
Sólo entonces se dio cuenta el Emperador de que lo colocase como lo colocase, la suma de los números de cada fila y de cada columna era siempre la misma: 15. De este modo, el dios Lo le había querido decir que el número de sacrificios necesario era 15. Ni uno más ni uno menos. Y gracias a la sabiduría del Emperador Yu las aguas del dios río Lo volvieron a su cauce.

- El mismo cuadrado al revés.
Así nació el primer cuadrado mágico de la historia, según la leyenda. Y en honor a ella, este cuadrado mágico (el más antiguo de todos los que existen) pasó a conocerse como Lo Shu: El libro del río Lo. Libro, porque para los antiguos chinos el cuadrado no se limitaba a expresar el número 15, sino que contenía en sí mismo la relación de armonía de los Elementos.
En las cuatro esquinas están los números pares ( Yin ), y los números impares (Yang) forman una cruz central. El número 5, que está en el centro, simboliza la Tierra, y los cinco elementos del universo oriental ( Agua, fuego, madera, metal y Tierra ) se representan por las parejas adyacentes: los metales (4 y 9), el fuego (2 y 7), el agua (1 y 6) y la madera (3 y 8).

- Lo Shu era la representación misma de la Armonía Universal para los Chinos. Como el Ying y el Yang, representa un equilibrio dinámico de fuerzas opuestas.
Matemática Recreativa.
Aunque los cuadrados mágicos dieron lugar el cálculo de matrices en matemáticas, hoy en día los han perdido aspecto sobrenatural y solo ha perdurado su faceta recreativa. Esto, en el fondo, es una contradicción, ya que el recreo es intrínsecamente sobrenatural: El origen etimológico de la palabra recreo es bastante evidente: volver a crear. De hecho, en su forma verbal, recrear conserva su sentido original de imitación. Un cuadro recrea una escena, una escultura recrea el volumen que ocupa (o que no ocupa, en el arte contemporaneo) un cuerpo. La diferencia entre crear y recrear marca también la frontera entre un dios y un ser humano. Sólo losdioses crean. Los hombres recrean. Y abandonarse al recreo es en el hombre una actividad análoga a la de los dioses en su labor de creación (algo que también ayuda a entender esa constante ociosidad de los dioses en el Olimpo. Para los griegos, esa actividad era creación en sí misma.
Así el hombre es feliz en su recreo, su recreación del mundo ha dado lugar, además de los juegos, a las artes, la ciencia y hasta la misma capacidad de expresión que nos da el lenguaje.
¿Pero qué tipo de cosas recrean los juegos matemáticos?. Pongamos como ejemplo un juego muy simple, uno de los juegos matemáticos más básicos que existen: El juego del 15. Consiste en sumar 15. Las reglas son las siguientes: Por turnos, cada uno de los dos jugadores dirá un número del 1 al 9, sin que se repita ninguno, y tratará de que los tres números sumen 15. Si no se consigue, se sigue jugando hasta que uno de los jugadores tenga tres números que sumen 15. No sólamente tendremos que pensar en nuestros números, sino también en los de nuestro oponente, con el fin de robárselos si éstos le conducen a la victoria. Por ejemplo: Yo escojo el 1. Mi oponente el 2. Yo el 5. Como mis números (5+1) suman 6, necesito un 9 (5+1+9=¡15!) en el turno siguiente para ganar, así que mi oponente está forzado a escojer el 9 para evitar que gane yo. Pero ahora sus números suman 11, así que yo estoy forzado a robarle el 4. Y así hasta que alguien gane o se agoten los nueve números (en cuyo caso la partida queda empatada).
Este juego es muy útil para desarrollar el cálculo mental de los niños que están aprendiendo a sumar. Pero ¿cómo podemos enseñar este juego a un niño que conoce los números pero aún no sabe sumar aún?. Eso es sencillo, ahora que conocemos el Lo Shu.





En el Juego del 15 debemos hallar tres números que sumen 15, propiedades (la de ser tres números y sumar 15) que cumplen todas las filas, columnas y diagonales de nuestro cuadrado mágico. Así pues, podemos reformular el mismo juego diciendo que debemos marcar tres casillas seguidas en la misma fila, columna o diagonal. Y, por supuesto, descubrimos en este punto que hemos estado jugando todo el rato al Tres en Raya:

El Tres en Raya es uno de los juegos más antiguos conocidos y el padre de todos los juegos de estrategia. Se han encontrado evidencias arqueológicas de que ya era practicado por los antiguos egipcios. A diferencia de los juegos de recorrido como el Senet, el Tres en Raya no busca recorrer una distancia, sino ocupar un espacio. El objetivo no es recorrer un tablero, sino dominarlo. Eso es lo que distingue a los juegos de estrategia de todos los demás.
Desde Egipto se extendió al resto del mundo, llegando a Asia, y los chinos debieron de quedar asombrados de la correspondencia entre el Tres en Raya y su recién descubierto cuadrado mágico. El descubrimiento no es ninguna trivialidad: Un comportamiento espacial puede ser descrito por una secuencia numérica. Dicho de otro modo: es posible la Geometría.
 Aplicando las ideas estratégicas adecuadas podemos jugar lo que se llama una partida perfecta. El problema del tres en raya es que si los dos jugadores juegan una partida perfecta el resultado es tablas. Dicho de otro modo: uno siempre puede forzar a su oponente a empatar. Por tanto, aunque el tres en raya contiene todos los elementos que hacen atractivo un juego de estrategia, tiene un gran defecto: La diversión es menor cuanto mejores sean los jugadores. No es extraño que en todo el mundo se modificase de un modo u otro tratando de conseguir que el placer del juego de estrategia se alargase lo más posible.
Aplicando las ideas estratégicas adecuadas podemos jugar lo que se llama una partida perfecta. El problema del tres en raya es que si los dos jugadores juegan una partida perfecta el resultado es tablas. Dicho de otro modo: uno siempre puede forzar a su oponente a empatar. Por tanto, aunque el tres en raya contiene todos los elementos que hacen atractivo un juego de estrategia, tiene un gran defecto: La diversión es menor cuanto mejores sean los jugadores. No es extraño que en todo el mundo se modificase de un modo u otro tratando de conseguir que el placer del juego de estrategia se alargase lo más posible.
Hay dos vías fundamentales por las que se intenta esa reforma:
Aparición de las fichas: Si en vez de marcar las casillas las ocupamos con un objeto ( piedras y conchas, que con el tiempo acabarían convirtiéndose en fichas) podemos evitar que se ocupen todas las casillas y esas fichas tendrán más alternativas para buscar el tres en raya. Aún así, el tablero se ve muy agobiado. Solo queda un espacio libre si jugamos con cuatro fichas, por lo que todos los movimientos serán forzados y se llega a bucles que vienen a ser un empate igualmente. Si reducimos el número de piezas a tres nos encontramos con una situación más despejada, pero en esencia, el problema es el mismo: Si los dos jugadores lo hacen bien sólo se puede conseguir un empate.
Como con menos de tres fichas no es posible hacer tres en raya, la siguiente solución es la ampliación de tablero. Los distintos tableros de los juegos Morris, o de los molinos, nos muestran cómo se intentan ampliar el número de distintos movimientos a base de ampliar el tablero.
La idea que subyace a esta s reformas es simple: cuantas más casillas podamos ocupar, más juegos posibles tendremos y más posibilidades de victoria. Pero aún así, no resolvemos el problema: en todos ellos se puede forzar el empate. Será necesario, pues, un análisis en mayor profundidad:
 Antes que nada hay que tener claro que los dos tableros que aparecen en la siguientes figuras A y B son exactamente iguales. La figura A descompone un espacio en una retícula, y la Figura B es un grafo de esa retícula. Luego el espacio se comporta del mismo modo tanto en A como en B .
Antes que nada hay que tener claro que los dos tableros que aparecen en la siguientes figuras A y B son exactamente iguales. La figura A descompone un espacio en una retícula, y la Figura B es un grafo de esa retícula. Luego el espacio se comporta del mismo modo tanto en A como en B .
Las posibles modificaciones del espacio en forma de retícula se limitan a añadir o sustraer filas y columnas, pero no influye en el comportamiento de las fichas. En cambio, las modificaciones de su grafo (fig.B) no modifica la división del espacio, sino el comportamiento de las fichas en éste (sus recorridos posibles).
Vemos por la diferencia entre los dos tableros de Three men’s Morris que existe una preocupación por el movimiento de las fichas. En uno, las fichas se pueden mover en todas direcciones. En otra no pueden moverse en diagonal (y tampoco vencer en esa alineacion).
Movimiento de una ficha aparece como un concepto nuevo en el juego. Antes sólamente existía la ocupación. Con la aparición de fichas móviles que tienen acceso a sus casillas contiguas hay un tema estratégico que gana importancia: el bloqueo. Si ocupamos todas las casillas adyacentes a una ficha enemiga, ésta quedará inmovilizada. Será, por tanto, completamente inutil. Este fenómeno gana en importancia cuanto mayores son el tablero y el número de piezas del juego y entorno a esta idea han evolucionado todos los juegos de la familia del Go, que considera una ficha rodeada como una ficha muerta.
Pero en las primeras ampliaciones que se producen (Six, Nine y Twelve Men Morris) el juego no consigue liberarse del empate forzado. Las ventajas conseguidas no acaban de materializarse nunca porque no existe aún ningún elemento en el juego que desequilibre la balanza de forma definitiva. ¿Y si el problema estuviese en ese equilobrio de fuerzas?. ¿Cómo llegar a conseguir tal desequilibrio si ambos jugadores tienen igual capacidad material hasta el final del juego?.
La aparición de la captura de piezas en los juegos de estrategia les llevaría a romper el empate forzado y llevó a una nueva familia de juegos que nada tendrían que ver con el Go. Pero esa revolución no habría sido posible si los que la llevaron a cabo no hubiesen tenido una comprensión profunda del espacio estratégico yt la esencia de la dominación. Tenemos testimonio de ello en el famoso libro El Arte de la Guerra, que escribió el general chino Sun Tzu y que por muchos ha sido considerado como el primer tratado de Go (hoy sus enseñanzas se aplican tanto en estrategia militar como en estrategia empresarial). Ese conocimiento del espacio estratégico llevaría a la constitución del ajedrez, pero lentamente fue cayendo en el olvido y se perdió hasta que en el siglo XX el propio ajedrez sufrió una revolución similar cuando una nueva escuela de jugadores encabezados por el singular Aaron Nimzowisch redescubrieron el espacio ajedrecístico en toda su profundidad. De estas dos revoluciones tan distantes en el tiempo y tan cercanas en su esencia trataremos en un capítulo a parte, antes de retomar el hilo y ser testigos del nacimiento de los movimientos de las piezas de ajedrez en la lejana China.
El tablero Chino:
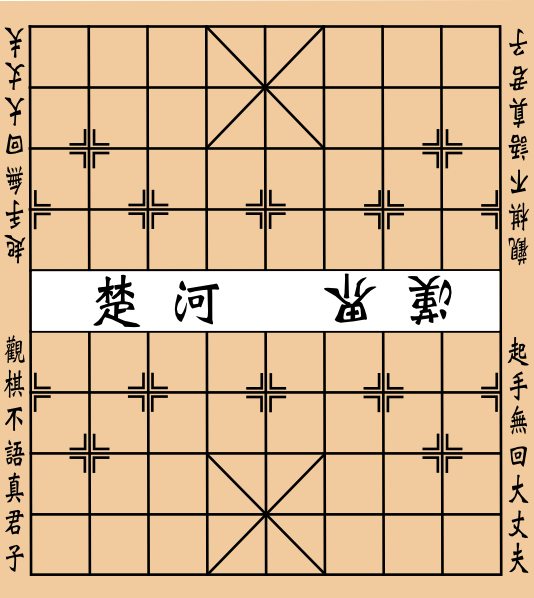
Cualquier intento de derivar el Xiangqi (o ajedrez chino) del Chaturanga está condenada al fracaso.

En primer lugar, el Xiangqi tiene un tablero propio en el que las piezas no se colocan en el interior de las casillas, sino en sus intersecciones. Otra de las diferencias más llamativas es que un río cruza horizontalmente el centro del tablero, separando los dos bandos e impidiendo el paso de algunas piezas. Por todo esto, resulta más coherente pensar que el Xiangqui pasó a la India adaptándose al tablero de Ashtapada que contrario: que del Ashtapada (un juego de recorrido) surgió de forma espontánea un juego de estrategia y éste pasó a China perdiendo su tablero original y adoptando uno nuevo en el que las piezas se colocan caprichosamente en las intersecciones y con el también caprichoso añadido de un río (¿será este el río Lo, del que salió la tortuga con el Lo Shu dibujado en el caparazón?). ¿No es mucho más sencillo que ese cambio obedezca de la adaptación del Xiangqi al tablero de Ashtapada, por no tener en la india otro tablero más parecido al original en el que jugar?
Aún asumiendo que las piezas de ajedrez y sus movimientos fueron exportadas a la India desde China, sin duda a través de la Ruta de la Seda, queda por explicar de dónde sale el Xiangqi, y esto nos va a llevar a un problema parecido al que nos encontramos en la India: El ajedrez, un juego de estrategia, parece evolucionar de un juego de recorrido. En este caso se trata del Liubo.

- Tablero de Liubo
Luibo es uno de los juegos más enigmáticos a los que se enfrentan los estudiosos. Hoy día se han perdido las reglas del juego, por lo que sólamente existen hipótesis. Precisamente este desconocimiento lo convierte en candidato perfecto a eslabón perdido, pues basta con construír una hipótesis medianamente verosímil para convertirlo en antecesor del juego que deseemos. Aún así, la mayoría de estudiosos coinciden en que, si no fue el antecesor, si tuvo una gran influencia en la formación del Xiangqi. Sea cual sea el grado de esta influencia, parece claro que es mayor en lo referente a las piezas que en el tablero. Aunque algunos han querido ver en el tablero de Luibo un paso intermedio entre Nine men Morris y Xiangqi, creo que sin más pruebas que la imaginación que uno pueda echarle, eso no pasa de mera especulación. Lo que si sabemos seguro es que Luibo era un juego de dos jugadores en el que cada uno tenía cinco piezas iguales y una distinta. Algunos han querido ver en ellas cinco peones y un rey al que defienden, lo que justificaría sobradamente su fama de predecesor del Xiangqi, pero para eso hay que justificar antes que se trataba de un juego de estrategia, y no de recorrido. Descgraciadamente, no hay pruebas concluyentes de lo uno ni de lo otro. Algunas teorías conciliadoras, como la de Cazaux, dicen que Luibo nació como juego de recorrido y se convirtió poco a poco en juego de estrategia. Pero si esto es así, ¿porqué no iba a ser posible tambien en el caso del Ashtapada?.
Como todo el mundo parece tener su hipótesis, aquí dejo yo la mía, sin pretender tener más ni menos razón que nadie: Existe una variedad de juegos a medio camino entre el juego de recorrido y el juego de estrategia: los juegos de caza. A esta familia pertenecen multitud de juegos como Fox and geese (Inglaterra), Fuchs und Gänse (Alemania), Renard et les poules (Francia) o la amplia categoría de juegos Tafl de los vikingos. Todos estos juegos consisten en que un depredador (uno de los jugadores) da caza a los animales de un rebaño (el otro jugador). El rasgo distintivo de estos juegos es la desigualdad entre los dos bandos. Por un lado está el depredador (una, dos o tres fichas a lo sumo) que puede capturar las piezas del contrincante. Por otro lado, el rebaño no puede capturar, pero si inmovilizar a los depredadores.
Los juegos de caza parecen derivar del Latrunculli romano (llamado Petteia por los griegos), aunque tambien existen versiones orientales como el Len Choa tailandés, lo que hace pensar en un antecesor común. Como ocurre con el Luibo, de la antigua roma nos llegan referencias confusas en las que a veces se describe al Latrunculli como un juego de recorrido y otras veces como un juego de estrategia. Cuando jugamos a alguno de los juegos de caza a los que ha dado lugar comprendemos la confusión. Un espectador casual no podría determinar si es lo uno o lo otro. Incluso un jugador que no comprenda con cierta profundidad la naturaleza del juego podría creer que el hecho de perseguir al contrincante lo convierte en un juego de recorrido con capturas. Sin embargo, en el fondo es un juego de estrategia en el que cada bando captura de un modo distinto. La idea de persecución es aquí casual, mientras que en los juegos de recorrido es esencial.
¿Podría ser Luibo uno de estos juegos?. En ese caso tendríamos, efectivamente, un juego de estrategia y la posibilidad de que el Xiangqi haya heredado algunos de sus rasgos fundamentales de Luibo; concretamente la idea de dar caza al Rey, que evolucionaría hasta convertirse jaque mate que fundamenta el ajedrez en todas sus variantes, por remotas que sean.

- Veamos el sospechoso parecido que guardan unos jugadores de Tafl y otros de Luibo
Hay que señalar que, a diferencia de los juegos de caza, en el Xiangqui todas las piezas capturan igual. La inmovilización de una pieza es algo casual. No así en el Go, que lo convierte en su único sistema de captura. Probablemente los juegos de caza surgieron en un periodo de transición, en la que los juegos de estrategia como los los morris empezaron a desarrollar distintos sistemas de captura y se oscilaba entre uno y otro.
Asumiendo que el Xiangqui tomó los peones y el rey de Luibo (o, al menos, de un juego de caza) aún quedan todas las demás piezas por explicar. Además, no sabemos cómo se movían las piezas en Luibo, pero es improbable que el rey y los peones del Xiangqi conservaran los movimientos que tenían en Luibo, dada la diferencia entre ambos tableros.
El movimiento de las piezas.
Volvamos al tablero de Tres en raya. Más concretamente, al cuadrado mágico Lo Shu. Hemos visto que para los antiguos Chinos era algo más que un simple cuadrado. No se trataba de algo estático, sino que las relaciones dinámicas que se producían entre sus distintas casillas eran la imagen misma de las relaciones dinámicas que se daban en el Universo. Lo importante, por tanto, no era el cuadrado en sí, sino las relaciones que se pueden dar en su interior y que, una vez surgidas piezas móviles, darán lugar a distintos tipos de movimientos. Veamos cuales son estas relaciones:

- Movimientos diagonal y ortogonal desde la casilla central
Si colocamos una ficha en la casilla central estará en contacto con todas las demás casillas del tablero. La relación que se establece puede ser ortogonal (cuando se trata dea una casilla que está en la misma fila o columna) o diagonal (cuando se trata de una casilla en distina fila y columna).

- Movimientos ortogonal y diagonal a larga distancia (desde cualquier casilla no central)
La principal característica de las casillas no centrales es que no estan en contacto con todas las demás casillas. Esto hace que algunos de sus movimientos posibles sean a larga distancia, es decir, a casillas con las que no están en contacto directo. Si atendemos a los dos tipos de movimiento vistos hasta ahora (ortogonal y diagonal) obtenemos como resultado de esta relación filas, columnas y diagonales. Es decir, las distintas formas de llegar al tres en raya. Sin embargo, si superponemos estos dos tipos de movimiento a larga distancia nos damos cuenta de que existe aún otro tipo de movimiento cuya característica es, precisamente, no ser ortogonal ni diagonal.

- Las casillas marcadas en rojo no tienen relación diagonal ni ortogonal con la casilla marcada con una X.
Este movimiento no solo ha fascinado a los jugadores de distintos juegos de estrategia durante más de mil años, sino también a matemáticos como Euler que lo conocieron, precisamente, a través del ajedrez. Es conocido con el nombre de salto de caballo (y así lo llamaremos en adelante también nosotros), precisamente porque de esta manera se mueve el caballo en ajedrez. Aunque en el Xiangqi la pieza no se trataba aún de un caballo, sino de un elefante.
Los movimientos ortogonal y diagonal (es decir, en filas, columnas y diagonales) son los que llevan al tres en raya, es decir: son movimientos de ataque. El movimiento de salto de caballo, en cambio, no conduce al tres en raya, por lo que su función en el juego sólo puede tener un sentido: bloquear el tres en raya del contrario. Esa naturaleza de bloqueador es algo que habrá que tener muy en cuenta a la hora de manejar el caballo en el ajedrez.
Sorprendentemente, esta relación entre casillas del tres en raya es muy parecida a los distintos movimientos de las piezas del Chaturanga. Pero más sorprendente aún es que coinciden exactamente con los movimientos de las piezas del ajedrez chino. Así que parece claro que el movimiento de las piezas se origina en China y viaja hasta la india, y no al revés.
Por tanto, el movimiento de las piezas de Xiangqi se podría esquematizar del siguiente modo:

- R=rey, A=alfil, C=caballo, V=visir
La casilla central, marcada con un aspa, es la ubicación de la pieza, y las casillas marcadas con una letra es dónde puede mover esa pieza. Si la pieza es un rey, podrá mover a las casillas marcadas con una R, si un caballo, a casillas marcadas con C, &c.
Corto alcance y largo alcance
La línea roja separa los movimientos a casillas contiguas de movimientos de largo alcance. Son piezas de corto alcance el rey y el visir (pieza que no existe en el ajedrez moderno y fue sustituído por la dama, de distinto movimiento, en la España de los Reyes Católicos dando lugar al ajedrez moderno) . Son piezas de largo alcance el alfíl y el caballo.
Los cuatro cuadrados grises se corresponden con un movimiento al que no corresponde ninguna pieza en el moderno Xiangqui, pero probablemente si en el antiguo, en el que existía una pieza hoy no utilizada llamada catapulta y que se correspondería con la torre de nuestro ajedrez (que, efectivamente, es la pieza de largo alcance con movimiento ortogonal que correspondería a esas casillas). Es significativo que esta pieza desapareciera de forma temprana, ya que es precisamente la torre la primera pieza en adoptar una nueva concepción de largo alcance que irá imponiéndose lentamente, a través de las distintas variantes de ajedrez, hasta llegar a la conformación del ajedrez moderno alrrededor del año 1500 d.C.
Esta transformación de la idea de largo alcance (que trataré con más detalle en otra ocasión) afectó también al alfíl y terminó convirtiendo al visir (pieza de corto alcance en un origen) en la Dama del ajedrez moderno: la pieza más poderosa sobre el tablero. De modo que los movimientos de las piezas en el ajedrez moderno que se juega hoy en día quedan establecidos del siguiente modo:

- Movimientos actuales de las piezas de largo alcance: Torre, Alfíl y Dama
Vemos, por tanto, que el tres en raya se encuentra ya el germen de los movimientos de las piezas de ajedrez y en Luibo da lugar a las únicas piezas que el tres en raya no puede explicar: los peones. Para entender la naturaleza del ajedrez hay que entender antes la naturaleza de los movimientos de sus piezas, qué finalidad persiguen sus movimientos y qué potencial estratégico esconde cada una. El valor de una pieza no es siempre el mismo, sino que cambia en distintos momentos de una partida. Esto es lo que en ajedrez se llama valor relativo de las piezas. Existen grandes discusiones teóricas acerca de este tema y los jugadores más fuertes no son precisamente los que mejor calculan posibles jugadas futuras, sino los que mejor saben valorar en el momento presente cada pieza. Más adelante estudiaremos detalladamente el valor de cada pieza, pero antes nos detendremos un momento a examinar el significado de los peones, la única pieza que no se origina en el tres en raya, dentro del ajedrez.
